Hi, CodeForces.↵
↵
Recently I decided to take a closer look at data structure called Fenwick tree or binary indexed tree.↵
↵
_In this blogpost I will only consider Fenwick tree for sum, but everything stated there can be easily generalized for any associative, commutative and inversable operation._↵
↵
<spoiler summary="Some implementation">↵
I will use 0-indexed Fenwick tree based on vectors (almost as it is implemented there [e-maxx.ru](http://e-maxx.ru/algo/fenwick_tree))↵
↵
~~~~~↵
vector<int> fenwick;↵
↵
void init_empty(int size_) {↵
fenwick.assign(size_, 0);↵
}↵
↵
int sum(int r) {↵
int res = 0;↵
↵
while (r >= 0) {↵
res += fenwick[r];↵
r = (r & (r+1)) - 1;↵
}↵
↵
return res;↵
}↵
↵
int sum(int l, int r) {↵
return sum(r) - sum(l-1);↵
}↵
↵
void inc(int i, int delta) {↵
while (i < fenwick.size()) {↵
fenwick[i] += delta;↵
i |= i+1;↵
}↵
}↵
~~~~~↵
↵
↵
</spoiler>↵
↵
After reading articles about it on [e-maxx.ru](http://e-maxx.ru/algo/fenwick_tree) and [neerc.ifmo.ru](https://neerc.ifmo.ru/wiki/index.php?title=Дерево_Фенвика) and asking friends I've got interested by this moment. Both articles (and my friends) use this algorithm to initialize Fenwick tree on given array:↵
↵
1. Fenwick tree for array of zeros is array of zeros, we will take it as a basis↵
2. We will use tree queries to replace all elements of array with elements we need↵
↵
~~~~~↵
void init_vector_classic (vector<int> a) {↵
init_empty(a.size());↵
↵
for (int i = 0; i < a.size(); i++) inc(i, a[i]);↵
}↵
~~~~~↵
↵
This will work in $O(N * log N)$ where $N$ is length of given array. ↵
↵
Can we do it faster? Definitely can!↵
↵
By definition of the Fenwick tree each tree element is the sum of continious segment of initial array. Considering that we have no queries to change elements in initialization process, we can use prefix sums to calculate elements of our Fenwick tree. This will require $O(N)$ preprocessing, but will allow to calculate tree elements in $O(1)$. So initialization asymptotic improves to $O(N) + O(1)*O(N) = O(N)$.↵
↵
~~~~~↵
void init_vector_linear_prefix (vector<int> a) {↵
init_empty(a.size());↵
↵
vector<int> prefix_sum;↵
prefix_sum.assign(a.size(), 0);↵
prefix_sum[0] = a[0];↵
for (int i = 1; i < a.size(); i++) prefix_sum[i] = prefix_sum[i-1] + a[i];↵
↵
for (int i = 0; i < a.size(); i++) {↵
int lower_i = (i & (i+1)) - 1;↵
fenwick[i] = prefix_sum[i] - (lower_i >= 0 ? prefix_sum[lower_i] : 0);↵
}↵
}↵
~~~~~↵
↵
But in this implementation we get additional $O(N)$ memory to store additional array.↵
↵
Can we avoid this? Yes, we can!↵
↵
We can notice that to initialize $fenwick[i]$ we only require such elements of $prefix\_ sum[j]$ where $j \leq i$. This allows to use only one array and, starting from the end, change each element from prefix sum to Fenwick tree element.↵
↵
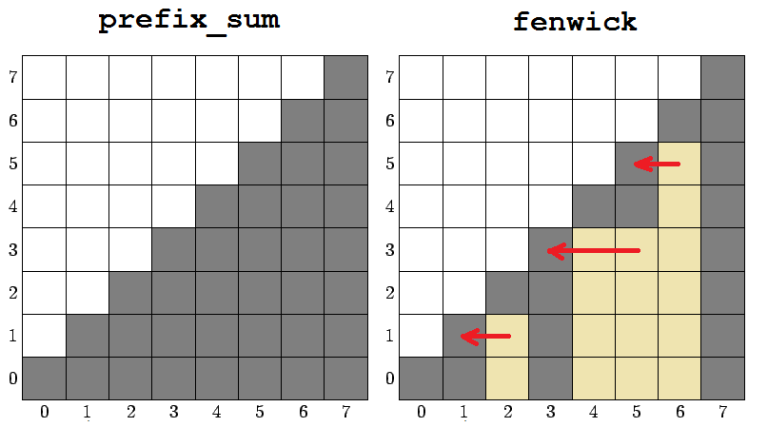↵
↵
~~~~~↵
void init_vector_linear (vector<int> a) {↵
init_empty(a.size());↵
↵
fenwick[0] = a[0];↵
for (int i = 1; i < a.size(); i++) fenwick[i] = fenwick[i-1] + a[i];↵
↵
for (int i = a.size()-1; i > 0; i--) {↵
int lower_i = (i & (i+1)) - 1;↵
if (lower_i >= 0) fenwick[i] -= fenwick[lower_i];↵
}↵
}↵
~~~~~↵
↵
This way we can improve initialization time of Fenwick tree to $O(N)$ using $O(1)$ additional memory.↵
↵
Of course, in most of the problems amount of queries is not much less than the size of Fenwick tree, so improving initialization time will not improve final asymptotic of your solution. But this optimization gives as ability to improve constant of the part of your solution, that works with Fenwick tree (or trees) with just a few lines of code.↵
↵
What do you think about this and how do you initialize your Fenwick trees?↵
↵
**UPD:** There is another approach to this problem that leads to even shorter code! Thanks [user:Jakube,2018-11-11] for mentioning this in comments and [user:sdnr1,2018-11-11] for [creating blog about it](https://codeforces.me/blog/entry/63064).↵
↵
Recently I decided to take a closer look at data structure called Fenwick tree or binary indexed tree.↵
↵
_In this blogpost I will only consider Fenwick tree for sum, but everything stated there can be easily generalized for any associative, commutative and inversable operation._↵
↵
<spoiler summary="Some implementation">↵
I will use 0-indexed Fenwick tree based on vectors (almost as it is implemented there [e-maxx.ru](http://e-maxx.ru/algo/fenwick_tree))↵
↵
~~~~~↵
vector<int> fenwick;↵
↵
void init_empty(int size_) {↵
fenwick.assign(size_, 0);↵
}↵
↵
int sum(int r) {↵
int res = 0;↵
↵
while (r >= 0) {↵
res += fenwick[r];↵
r = (r & (r+1)) - 1;↵
}↵
↵
return res;↵
}↵
↵
int sum(int l, int r) {↵
return sum(r) - sum(l-1);↵
}↵
↵
void inc(int i, int delta) {↵
while (i < fenwick.size()) {↵
fenwick[i] += delta;↵
i |= i+1;↵
}↵
}↵
~~~~~↵
↵
↵
</spoiler>↵
↵
After reading articles about it on [e-maxx.ru](http://e-maxx.ru/algo/fenwick_tree) and [neerc.ifmo.ru](https://neerc.ifmo.ru/wiki/index.php?title=Дерево_Фенвика) and asking friends I've got interested by this moment. Both articles (and my friends) use this algorithm to initialize Fenwick tree on given array:↵
↵
1. Fenwick tree for array of zeros is array of zeros, we will take it as a basis↵
2. We will use tree queries to replace all elements of array with elements we need↵
↵
~~~~~↵
void init_vector_classic (vector<int> a) {↵
init_empty(a.size());↵
↵
for (int i = 0; i < a.size(); i++) inc(i, a[i]);↵
}↵
~~~~~↵
↵
This will work in $O(N * log N)$ where $N$ is length of given array. ↵
↵
Can we do it faster? Definitely can!↵
↵
By definition of the Fenwick tree each tree element is the sum of continious segment of initial array. Considering that we have no queries to change elements in initialization process, we can use prefix sums to calculate elements of our Fenwick tree. This will require $O(N)$ preprocessing, but will allow to calculate tree elements in $O(1)$. So initialization asymptotic improves to $O(N) + O(1)*O(N) = O(N)$.↵
↵
~~~~~↵
void init_vector_linear_prefix (vector<int> a) {↵
init_empty(a.size());↵
↵
vector<int> prefix_sum;↵
prefix_sum.assign(a.size(), 0);↵
prefix_sum[0] = a[0];↵
for (int i = 1; i < a.size(); i++) prefix_sum[i] = prefix_sum[i-1] + a[i];↵
↵
for (int i = 0; i < a.size(); i++) {↵
int lower_i = (i & (i+1)) - 1;↵
fenwick[i] = prefix_sum[i] - (lower_i >= 0 ? prefix_sum[lower_i] : 0);↵
}↵
}↵
~~~~~↵
↵
But in this implementation we get additional $O(N)$ memory to store additional array.↵
↵
Can we avoid this? Yes, we can!↵
↵
We can notice that to initialize $fenwick[i]$ we only require such elements of $prefix\_ sum[j]$ where $j \leq i$. This allows to use only one array and, starting from the end, change each element from prefix sum to Fenwick tree element.↵
↵
↵
↵
~~~~~↵
void init_vector_linear (vector<int> a) {↵
init_empty(a.size());↵
↵
fenwick[0] = a[0];↵
for (int i = 1; i < a.size(); i++) fenwick[i] = fenwick[i-1] + a[i];↵
↵
for (int i = a.size()-1; i > 0; i--) {↵
int lower_i = (i & (i+1)) - 1;↵
if (lower_i >= 0) fenwick[i] -= fenwick[lower_i];↵
}↵
}↵
~~~~~↵
↵
This way we can improve initialization time of Fenwick tree to $O(N)$ using $O(1)$ additional memory.↵
↵
Of course, in most of the problems amount of queries is not much less than the size of Fenwick tree, so improving initialization time will not improve final asymptotic of your solution. But this optimization gives as ability to improve constant of the part of your solution, that works with Fenwick tree (or trees) with just a few lines of code.↵
↵
What do you think about this and how do you initialize your Fenwick trees?↵
↵
**UPD:** There is another approach to this problem that leads to even shorter code! Thanks [user:Jakube,2018-11-11] for mentioning this in comments and [user:sdnr1,2018-11-11] for [creating blog about it](https://codeforces.me/blog/entry/63064).↵






