You are given $$$n$$$ rectangles on a plane with coordinates of their bottom left and upper right points. Some $$$(n-1)$$$ of the given $$$n$$$ rectangles have some common point. A point belongs to a rectangle if this point is strictly inside the rectangle or belongs to its boundary.
Find any point with integer coordinates that belongs to at least $$$(n-1)$$$ given rectangles.
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 132\,674$$$) — the number of given rectangles.
Each the next $$$n$$$ lines contains four integers $$$x_1$$$, $$$y_1$$$, $$$x_2$$$ and $$$y_2$$$ ($$$-10^9 \le x_1 < x_2 \le 10^9$$$, $$$-10^9 \le y_1 < y_2 \le 10^9$$$) — the coordinates of the bottom left and upper right corners of a rectangle.
Print two integers $$$x$$$ and $$$y$$$ — the coordinates of any point that belongs to at least $$$(n-1)$$$ given rectangles.
3
0 0 1 1
1 1 2 2
3 0 4 1
1 1
3
0 0 1 1
0 1 1 2
1 0 2 1
1 1
4
0 0 5 5
0 0 4 4
1 1 4 4
1 1 4 4
1 1
5
0 0 10 8
1 2 6 7
2 3 5 6
3 4 4 5
8 1 9 2
3 4
The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.

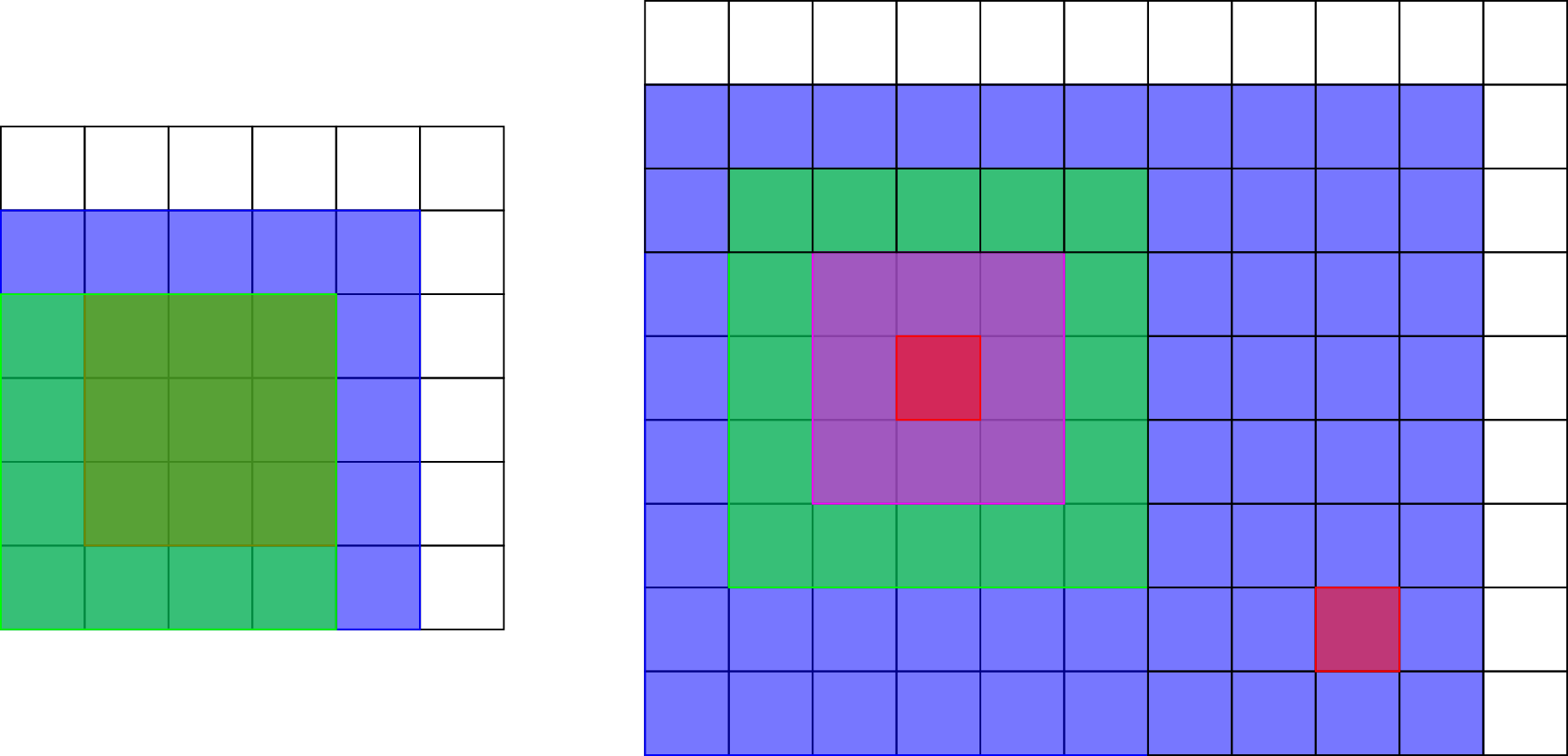
The picture below shows the rectangles in the third and fourth samples.
| Name |
|---|




