| Codeforces Round 372 (Div. 1) |
|---|
| Закончено |
Кодер ZS нарисовал неориентированный граф из n вершин пронумерованных от 0 до n - 1 и m ребер между ними. Каждое ребро графа взвешено, а каждый вес — целое положительное число.
На следующий день Кодер ZS обнаружил, что некоторые из весов были стерты! Теперь он хочет восстановить целый положительный вес у каждого ребра, вес которого был стерт, так, что длина кратчайшего пути между вершинами s и t в получившемся графе в точности равна L. Поможете ему?
Первая строка содержит пять целых чисел n, m, L, s, t (2 ≤ n ≤ 1000, 1 ≤ m ≤ 10 000, 1 ≤ L ≤ 109, 0 ≤ s, t ≤ n - 1, s ≠ t) — количество вершин, количество ребер, желаемая длина кратчайшего пути, начальная и конечная вершины соответственно.
Далее следуют m строк, описывающие ребра графа. i-ая из них содержит три целых числа ui, vi, wi (0 ≤ ui, vi ≤ n - 1, ui ≠ vi, 0 ≤ wi ≤ 109). ui и vi означают концы ребра, а wi — его вес. Если wi равно 0, то вес соответствующего ребра был стерт.
Гарантируется, что между каждой парой вершин существует не более одного ребра.
Выведите «NO» (без кавычек) в единственной строке, если восстановить веса ребрам требуемым образом невозможно.
В противном случае, выведите «YES» в первой строке. Следующие m строк должны содержать описания ребер получившегося графа, с весами, заданными ребрам, вес которых был стерт. i-ая из них должна содержать три целых числа ui, vi и wi, означающих ребро между ui и vi веса wi. Ребра нового графа должны совпадать с ребрами графа из входных данных. Веса, которые не были стерты, должны остаться неизменными, тогда как новые веса могут быть любыми целыми положительными числами, не превышающими 1018.
Порядок ребер в выходных данных не важен. Длина кратчайшего пути между s и t должна равняться L.
Если существует несколько решений, выведите любое из них.
5 5 13 0 4
0 1 5
2 1 2
3 2 3
1 4 0
4 3 4
YES
0 1 5
2 1 2
3 2 3
1 4 8
4 3 4
2 1 123456789 0 1
0 1 0
YES
0 1 123456789
2 1 999999999 1 0
0 1 1000000000
NO
Вот так выглядит граф в первом примере из условия:
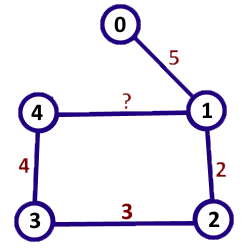
В первом примере из условия вес отсутствует всего у одного ребра. Если задать ему вес, равный 8, то длина кратчайшего пути между 0 и 4 будет равна 13.
Во втором примере из условия всего одно ребро. Очевидно, единственным ответом является задание ему веса 123456789.
В последнем примере из условия ни один вес задавать не нужно, но длина кратчайшего пути не совпадает с нужным значением, так что ответ — «NO».
| Название |
|---|




