C. Граф инверсий
ограничение по времени на тест
1 секунда
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Вам дана перестановка $$$p_1, p_2, \dots, p_n$$$. Затем вы строите неориентированный граф следующим образом: добавляется ребро между вершинами $$$i$$$, $$$j$$$ такими, что $$$i < j$$$ тогда и только тогда, когда $$$p_i > p_j$$$. Вам нужно посчитать количество компонент связности в этом графе.

Две вершины $$$u$$$ и $$$v$$$ принадлежат одной компоненте связности тогда и только тогда, когда существует хотя бы один путь по рёбрам графа, соединяющий $$$u$$$ и $$$v$$$.

Перестановкой называется массив, состоящий из $$$n$$$ различных целых чисел от $$$1$$$ до $$$n$$$ в произвольном порядке. Например, $$$[2,3,1,5,4]$$$ является перестановкой, но $$$[1,2,2]$$$ не является перестановкой ($$$2$$$ встречается дважды в массиве) и $$$[1,3,4]$$$ тоже не является перестановкой ($$$n=3$$$, но $$$4$$$ присутствует в массиве).

Входные данные

Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.

В первой строке каждого набора входных данных содержится целое число $$$n$$$ ($$$1 \le n \le 10^5$$$) — длина перестановки.

Во второй строке каждого набора входных данных содержатся $$$n$$$ целых чисел $$$p_1, p_2, \dots, p_n$$$ ($$$1 \le p_i \le n$$$) — элементы перестановки.

Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.

Выходные данные

Для каждого набора входных данных выведите одно целое число $$$k$$$ — количество компонент связности.

Пример
Входные данные
6
3
1 2 3
5
2 1 4 3 5
6
6 1 4 2 5 3
1
1
6
3 2 1 6 5 4
5
3 1 5 2 4
Выходные данные
3
3
1
1
2
1
Примечание

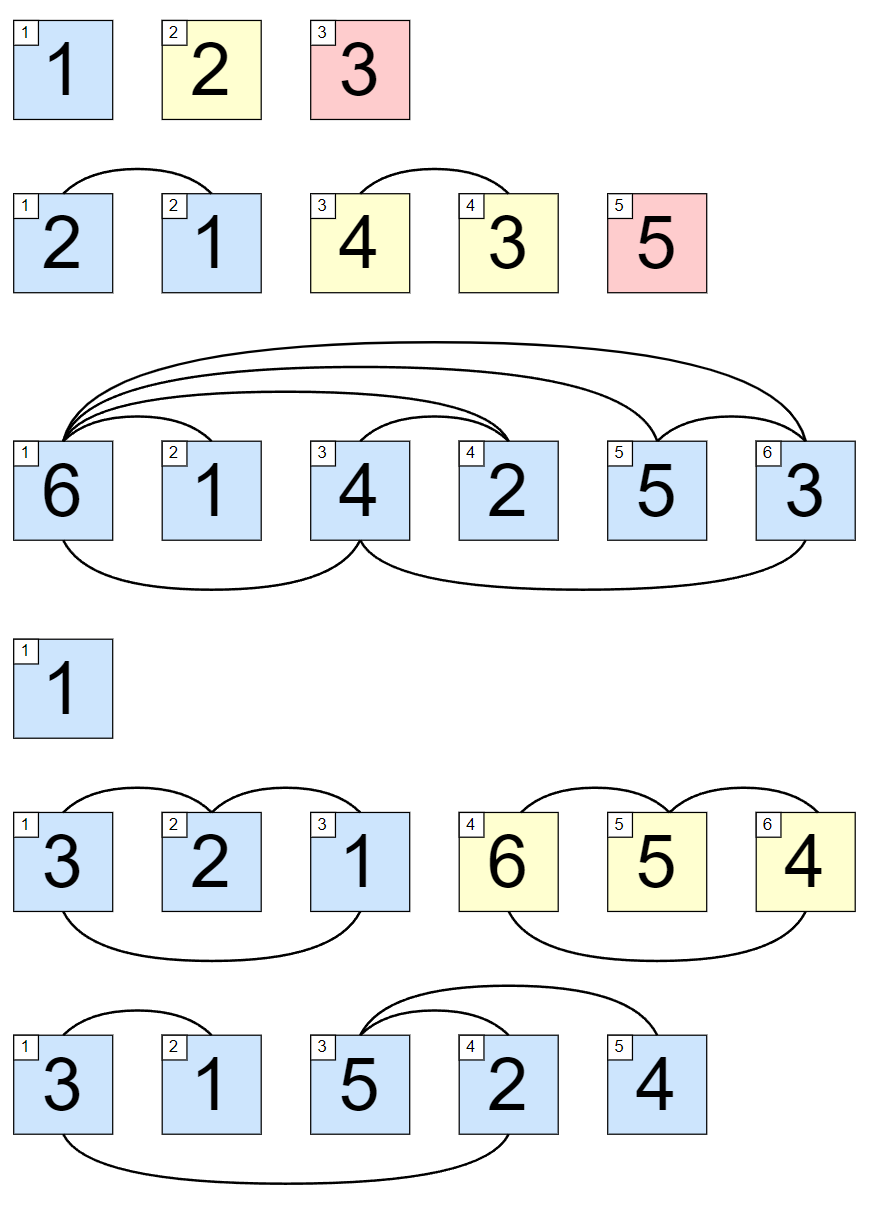
Каждый отдельный набор входных данных изображен на картинке ниже. Цветные квадраты представляют собой элементы перестановки. Для одной перестановки каждый цвет представляет некоторую компоненту связности. Ответом является количество различных цветов.