| Codeforces Round 473 (Div. 2) |
|---|
| Finished |
Ehab is interested in the bitwise-xor operation and the special graphs. Mahmoud gave him a problem that combines both. He has a complete graph consisting of n vertices numbered from 0 to n - 1. For all 0 ≤ u < v < n, vertex u and vertex v are connected with an undirected edge that has weight  (where
(where  is the bitwise-xor operation). Can you find the weight of the minimum spanning tree of that graph?
is the bitwise-xor operation). Can you find the weight of the minimum spanning tree of that graph?
You can read about complete graphs in https://en.wikipedia.org/wiki/Complete_graph
You can read about the minimum spanning tree in https://en.wikipedia.org/wiki/Minimum_spanning_tree
The weight of the minimum spanning tree is the sum of the weights on the edges included in it.
The only line contains an integer n (2 ≤ n ≤ 1012), the number of vertices in the graph.
The only line contains an integer x, the weight of the graph's minimum spanning tree.
4
4
In the first sample: 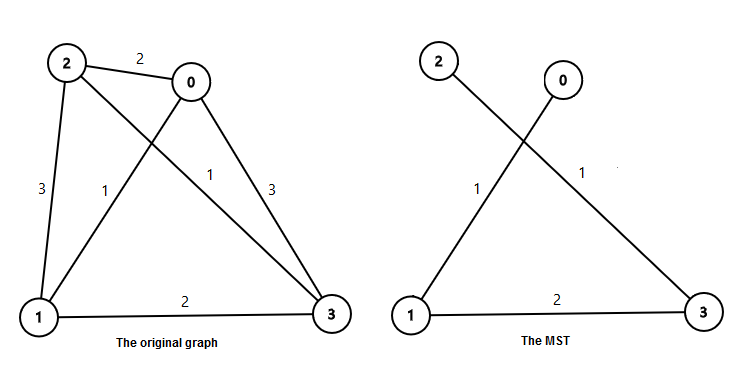 The weight of the minimum spanning tree is 1+2+1=4.
The weight of the minimum spanning tree is 1+2+1=4.
| Name |
|---|




