| Codeforces Global Round 18 |
|---|
| Закончено |
Это была ночь перед рождеством, и пришло время Санте украсить свое Рождественское дерево. Это дерево состоит из $$$n$$$ вершин, соединенных $$$n-1$$$ ребром. На каждом ребре дерева расположена гирлянда, которую можно описать некоторым числом в двоичном представлении.
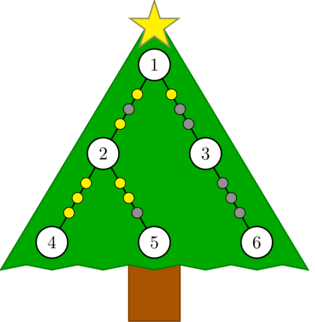
Посмотреть на это дерево собралось $$$m$$$ эльфов. Каждый эльф выбрал две вершины $$$a$$$ и $$$b$$$, и он смотрит только на гирлянды на простом пути между этими вершинами. В результате созерцания у эльфа появляется любимое число, равное побитовому исключающему ИЛИ значений на ребрах этого пути.
Однако, Северный Полюс только начал восстанавливаться после недавней эпидемии ОРВИ. Из-за этого Санта успел забыть, как выглядели некоторые гирлянды, и проверить их он не может, потому что уже покинул Северный Полюс! К счастью, на помощь пришли эльфы: каждый из них сообщил Санте свою пару вершин $$$(a_i, b_i)$$$, и четность количества единичных битов в своем любимом числе. Другими словами, каждый эльф помнит, было ли количество $$$1$$$-ц в его любимом числе, записанном в двоичном виде, четным или нечетным.
Помогите Санте проверить, могло ли существовать такое дерево, и если да, как оно могло выглядеть, и возможно вы войдете в историю!
В первой строке задано одно целое число $$$t$$$ ($$$1 \leq t \leq 2 \cdot 10^4$$$) — количество наборов входных данных. Далее следуют $$$t$$$ наборов входных данных.
В первой строке каждого набора заданы два целых числа $$$n$$$ и $$$m$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$; $$$1 \leq m \leq 2 \cdot 10^5$$$) — размер дерева и количество эльфов, соответственно.
В следующих $$$n-1$$$ строках каждого набора заданы по три целых числа $$$x$$$, $$$y$$$ и $$$v$$$ ($$$1 \leq x, y \leq n$$$; $$$-1 \leq v < 2^{30}$$$), описывающих ребро между вершинами $$$x$$$ и $$$y$$$. Если
- $$$v = -1$$$, то Санта не помнит как выглядит гирлянда на этом ребре.
- $$$v \geq 0$$$, то состояние гирлянды равно $$$v$$$.
В следующих $$$m$$$ строках каждого набора заданы по три целых числа $$$a$$$, $$$b$$$ и $$$p$$$ ($$$1 \leq a, b \leq n$$$; $$$a \neq b$$$; $$$0 \leq p \leq 1$$$) — пара вершин выбранная эльфом и четность количества единичных битов в любимом числе эльфа.
Гарантируется, что сумма $$$n$$$ и сумма $$$m$$$ по всем наборам не превосходят $$$2 \cdot 10^5$$$ (каждая).
Гарантируется, что заданные ребра образуют дерево.
Для каждого набора входных данных, сначала выведите YES или NO (в любом регистре), в зависимости от того, существует ли дерево, соответствующее памяти Санты, или нет.
Если ответ YES, выведите $$$n-1$$$ строк по три целых числа в каждом: $$$x$$$, $$$y$$$ и $$$v$$$ ($$$1 \le x, y \le n$$$; $$$0 \le v < 2^{30}$$$) — ребро дерева и число, описывающее состояние гирлянды на нем. Множество ребер должно совпадать с множеством из входных данных, и если состояние гирлянды на ребре известно, то оно не должно измениться. Вы можете выводить ребра в любом порядке.
Если существует несколько решений, выведите любое.
4 6 5 1 2 -1 1 3 1 4 2 7 6 3 0 2 5 -1 2 3 1 2 5 0 5 6 1 6 1 1 4 5 1 5 3 1 2 -1 1 3 -1 1 4 1 4 5 -1 2 4 0 3 4 1 2 3 1 3 3 1 2 -1 1 3 -1 1 2 0 1 3 1 2 3 0 2 1 1 2 1 1 2 0
YES 1 2 0 1 3 1 2 4 7 3 6 0 2 5 0 YES 1 2 1 1 3 0 1 4 1 4 5 1 NO NO
Первый набор входных данных соответствует изображению из условия.
Один из возможных ответов — это присвоить ребру $$$(1, 2)$$$ значение $$$5$$$, а ребру $$$(2, 5)$$$ — значение $$$3$$$. Этот способ подходит потому что:
- Первый эльф рассматривает путь между вершинами $$$2$$$ и $$$3$$$. Его любимое число будет равно $$$4$$$, а потому он помнит значение $$$1$$$ (так как в двоичном представлении $$$4$$$ нечетное количество битов $$$1$$$).
- Второй эльф рассматривает путь между вершинами $$$2$$$ и $$$5$$$. Его любимое число будет равно $$$3$$$, а потому он помнит значение $$$0$$$ (так как в двоичном представлении $$$3$$$ четное количество битов $$$1$$$).
- Третий эльф рассматривает путь между вершинами $$$5$$$ и $$$6$$$. Его любимое число будет равно $$$7$$$, а потому он помнит значение $$$1$$$ (так как в двоичном представлении $$$7$$$ нечетное количество битов $$$1$$$).
- Четвертый эльф рассматривает путь между вершинами $$$6$$$ и $$$1$$$. Его любимое число будет равно $$$1$$$, а потому он помнит значение $$$1$$$ (так как в двоичном представлении $$$1$$$ нечетное количество битов $$$1$$$).
- Пятый эльф рассматривает путь между вершинами $$$4$$$ и $$$5$$$. Его любимое число будет равно $$$4$$$, а потому он помнит значение $$$1$$$ (так как в двоичном представлении $$$4$$$ нечетное количество битов $$$1$$$).
Заметим, что существуют и другие возможные ответы.
| Название |
|---|




