| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
392. Cyclic Troubles
Time limit per test: 1 second(s)
Memory limit: 65536 kilobytes
Memory limit: 65536 kilobytes
input: standard
output: standard
output: standard
A package has been delivered to the King of Berland containing a game called "Bercycles". It's an entertaining single-player game with simple rules:
- You're given a rectangular field consisting of R rows and C columns, which result in R*C cells total. Each cell contains a lowercase Latin letter and an arrow pointing one of the four following directions: left, right, up, or down.
- You choose the cell at which you wish to start the game and make a number of moves. At each move you have to write down the letter from the current cell and move one cell in the direction shown by the arrow at this cell. You can stop moving any time you want. If you leave the field, the process stops automatically and you're not allowed to move anymore.
- The letters you write down during your movements form a word that you read during the game.
After reading the rules the King of Berland realized that he is in trouble. He is given a number of words and for each word he is to determine whether it is possible to play the game and read this word. Please help the King to solve this challenging problem.
Input
The first line of input file contains integer numbers R and C (1 ≤ R ≤ 30, 1 ≤ C ≤ 30) — number of rows and columns correspondingly. The following R lines describe arrows on the field. Each of these R lines contains exactly C characters. Each character denotes a direction:- '
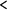 ' character - LEFT
' character - LEFT - '
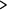 ' character - RIGHT
' character - RIGHT - '
 ' character - UP
' character - UP - '
 ' character - DOWN
' character - DOWN
Then R more lines follow, describing letters on the field. Each of these R lines contains exactly C characters. Each character is a lowercase Latin letter 'a'-'z'.
Then one more line follows containing a single integer number Q (1 ≤ Q ≤ 50) — number of queries. Each of the following Q lines contains a word for which you should solve the problem.
To reduce the size of input files, these Q words are given to you in a compressed form. A compressed form of a word may contain non-empty letter sequence F enclosed in parentheses, followed by a positive integer number K. It means that the fragment F should be repeated K times.
For example, the string "a(xy)2y(ab)3abz" is one of the compressed forms of the string "axyxyyababababz". Note: parentheses may not be enclosed into each other, so "a(xy)2y((ab)2)2z" is not a compressed form of the same word. Leading zeroes are not allowed as well in a compressed form, so no queries like "(ab)02" will be given to you.
Input file will not contain any malformed compressed words. The length of each compressed query will be between 1 and 2000 characters. When decompressed, the length of each query will be no longer than 109 characters.
Output
For each query you should print a single line to the output file. If the corresponding compressed word can be read on the field, then the line should contain "YES (X,Y)", where X and Y correspond to the row and column in the field where you should start in order to read the given word. Rows and columns are numbered starting from 1.If the word can't be found in the field, you should print a single word "NO" in the line. If there is more than one solution, print the one with a minimal row X. If there is more than one solution with the same minimal row, print one that minimizes column Y. Please see sample output for further clarifications on the output file format.
Example(s)
sample input | sample output |
2 4 >>>v <^<< abcd efgh 6 abcdhgf bcdhgf (bcdhgf)100 a(bcdhgf)100bc b(cdhgfbc)1d hello | YES (1,1) YES (1,2) YES (1,2) YES (1,1) YES (1,2) NO |
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 09:54:34 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




