| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
381. Bidirected Graph
Time limit per test: 0.5 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
The notion of bidirected graphs is used to formulate and solve wide range of combinatorial optimization problems: matchings, b-matchings, T-joins, T-paths packing and so on. Bidirected graph is a generalization of directed graph, where every arc has two orientations — one for every end.
More formally, bidirected graph is a tuple (V, E, ends, ω). V is a set of nodes, E is a set of edges, ends is a mapping from E: ends(e) = {u, v}, where u, v ∈ V, u ≠ v. For every e ∈ E and v ∈ ends(e) we define ω(e, v) ∈ {-1, +1}. It is called the direction of the edge e in the node v.
An s-t walk in a bidirected graph G is an alternating sequence
P = (s = v0, e1, v1,..., ek, vk = t),
where vi ∈ V, ei ∈ E, ends(ei) = {vi - 1, vi} and ω(ei + 1, vi) ω(ei, vi) = -1.
A directed graph without loops can be considered as bidirected, if we replace each arc a = (u, v) with an edge ea, and put ends(ea) = {u, v}, ω(ea, u) = -1, ω(ea, v) = +1.
An elementary transformation on node v is defined as follows: if for e ∈ E, ω(e, v) is defined, then negate it. It's clear that elementary transformations don't change the set of walks in G.
We want to determine if it is possible to convert bidirected graph to "directed" graph (i.e. to graph that can be obtained from some directed graph by means of the consideration described above) using several elementary transformations. If it is, we also want to know how to do it using the minimal number of elementary transformations.
Input
The first line of the input contains two integer numbers n and m — the number of vertices and the number of edges in the graph (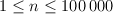 ,
, 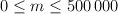 ). Next m lines describe the edges of the graph. Each line consists of four numbers ai, bi, di,1, di,2, where ai and bi are the ends of the egde e and di,1=ω(e,ai), di,2=ω(e,bi); 1 ≤ ai, bi ≤ n, di,j ∈ {-1, 1}.
). Next m lines describe the edges of the graph. Each line consists of four numbers ai, bi, di,1, di,2, where ai and bi are the ends of the egde e and di,1=ω(e,ai), di,2=ω(e,bi); 1 ≤ ai, bi ≤ n, di,j ∈ {-1, 1}.Output
If it is impossible to perform required transformation, output should contain exactly one string "NO" (quotes for clarity only). Otherwise, the first line should contain string "
YES", the second line should contain the number of elementary transformations in your solution, and the following lines should describe those transformations. Each transformation should be described by exactly one number — the index of the vertex of this transformation. If there are several answers with the minimal number of transformations, output any of them.
Example(s)
sample input | sample output |
4 3 1 3 -1 -1 2 3 -1 -1 3 4 1 1 | YES 1 3 |
sample input | sample output |
3 3 1 2 1 1 2 3 1 1 1 3 1 1 | NO |
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/19/2025 01:42:03 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




