| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
371. Subway
Time limit per test: 0.5 second(s)
Memory limit: 65536 kilobytes
Memory limit: 65536 kilobytes
input: standard
output: standard
output: standard
You need to create the plan of building subway in the city of S***. The subway must consist of some circle lines, each consisting of three or more stations, up to ten stations. Each circle line must be linked as a loop: first station is linked with second, second with third and so on. The circle lines themselves are linked as a chain: changing from one circle line to another is possible only at one station for each consecutive pair of circle lines in that chain. Other pairs of circle lines have no intersections. Any non-degenerate segment of subway is allowed to be contained only by one circle line.
Also it is needed to add radial lines, which start on some stations of circle lines and go to the distant parts of city. Unfortunately, due to lack of funds, radial line is allowed to consist only of two stations, one of them connects the radial line to circle line, and the other station is the terminal station. Terminal station cannot lie on more than one line. Any transfer station, which connects any two lines, could not connect more than two lines. No two radial lines are allowed to have common stations.
It is required to build exactly N stations and M segments between stations. Your task is to find the plan.
Input
First line contains two integers N and M (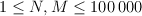 ).
).Output
First line must contain the number of circle lines K. K lines follow, each describing one circle line. Circle line is described by the number of stations on it, then the station numbers themselves in traversing order. The next line contains R — the number of radial lines. R last lines contain pairs describing radial lines. All stations are numbered from 1 to N. Your plan must consist of exactly N stations and M connecting segments. If there is no solution, output "No solution" without quotes.
Example(s)
sample input | sample output |
12 14 | 3 3 1 2 3 3 4 5 6 4 3 7 4 8 4 1 9 2 10 11 5 12 6 |
sample input | sample output |
4 3 | No solution |
Picture describing the first sample
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 10:09:44 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




