| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
352. Beerland Attacks
Time limit per test: 0.5 second(s)
Memory limit: 65536 kilobytes
Memory limit: 65536 kilobytes
input: standard
output: standard
output: standard
In this task Berland again needs your help. Berland consists of N cities. Some pairs of the cities are connected by bidirectional roads. Each road is characterized by its length. The cities are numbered from 1 to N, the capital has number 1. From time to time the President of Beerland takes a tour around the country visiting all the cities. The tour is a sequence of trips. The goal of each trip is to visit one of the cities and return to the capital. During the trip the President chooses one of the shortest ways from the capital to the desired city.
Long time ago, when Dijkstra algorithm seemed to be difficult, the royal security service created a secret set of roads T. Security officers created the T set in such a manner that it is possible to get by the shortest way from the capital to any city using only roads from the set T. Moreover, there is only one way from the capital to each city along the roads from the T set. The smartest citizens called this set "tree of the shortest paths".
The President uses only roads from the T set during his trips. With years passing the set lost much of its secrecy. Moreover, recently Beerland extremists have come into possesion of the secret set.
Now the royal security service has the new task. For each city except the capital it is required to find out vi (2≤ i≤ N), where vi is the length of the shortest path to the i-th city if the last road on the way to this city is attacked and the President can't use it any more.
Input
The first line of the input contains two integer numbers N and M (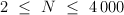 ;
; 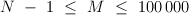 ), where N is a number of the cities in the country and m is a number of the roads. The following M lines contain the description of the roads, one per line. Each road description is given as the four integer numbers aj, bj, lj, tj, where aj, bj are numbers of the cities connected by the road (1 ≤ aj,bj ≤ n; aj <> bj), lj — length of the road (1 ≤ lj ≤ 105), tj is equal to 1 if the road belongs to the shortest paths tree T and to 0 otherwise.
), where N is a number of the cities in the country and m is a number of the roads. The following M lines contain the description of the roads, one per line. Each road description is given as the four integer numbers aj, bj, lj, tj, where aj, bj are numbers of the cities connected by the road (1 ≤ aj,bj ≤ n; aj <> bj), lj — length of the road (1 ≤ lj ≤ 105), tj is equal to 1 if the road belongs to the shortest paths tree T and to 0 otherwise.The given set T satisfies the requirements listed in the problem statement. There can be more than one road between a pair of cities. All roads are bidirectional.
Output
Write to the output N-1 numbers separated by spaces. i-th number should be equal to the length of the shortest way from the capital to the city i+1 or -1 if the way doesn't exist.Example(s)
sample input | sample output |
5 9 3 1 3 1 1 4 2 1 2 1 6 0 2 3 4 0 5 2 3 0 3 2 2 1 5 3 1 1 3 5 2 0 4 5 4 0 | 6 7 8 5 |
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 10:04:24 (l3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




