| acmsguru |
|---|
| Finished |
→ Problem tags
*special problem
No tag edit access
The problem statement has recently been changed. View the changes.
×
248. Integer Linear Programming
time limit per test: 0.25 sec.
memory limit per test: 65536 KB
memory limit per test: 65536 KB
input: standard
output: standard
output: standard
You are to solve some problem of integer linear programming. It is posed in the following way. Let x[i] be a variable which is required to be a non-negative integer (for any i from [1..N]). The goal is to minimize the function f(x[1], x[2],..., x[N])=x[1]+x[2]+...+x[N] (objective function) satisfying the constraint c[1]*x[1]+c[2]*x[2]+...+c[N]*x[N]=V.
The point X=(x[1], x[2],..., x[N]) that satisfies the constraint is called "feasible". All feasible points form a feasible set.
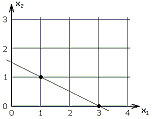
To make things clear, let us consider the following example N=2, c[1]=2, c[2]=4, V=6. There are only two feasible points: (1, 1) and (3, 0).
Clearly, the point (1, 1) is the optimal solution, because f(1, 1)<f(3, 0).
The point X=(x[1], x[2],..., x[N]) that satisfies the constraint is called "feasible". All feasible points form a feasible set.
To make things clear, let us consider the following example N=2, c[1]=2, c[2]=4, V=6. There are only two feasible points: (1, 1) and (3, 0).
Clearly, the point (1, 1) is the optimal solution, because f(1, 1)<f(3, 0).
Input
The first line of input contains a single positive integer N (0<N<=3). The second line contains N positive integers c[i] separated by whitespaces (0<c[i]<=10^6). The last line contains positive integer V (0<V<=10^6).
Output
On the first line of the output file print the minimal possible value of the function f, or "-1" (without quotes) if the problem has no solution.
Sample test(s)
Input
Test #1
2
2 4
6
Test #2
2
7 4
9
2
2 4
6
Test #2
2
7 4
9
Output
Test #1
2
Test #2
-1
2
Test #2
-1
Note
See picture:

| Author: | Dmitry Filippov (DEF) |
| Resource: | Petrozavodsk Summer Training Sessions 2004 |
| Date: | August 25, 2004 |
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/19/2025 02:04:58 (l3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




