D. Friends and Subsequences
time limit per test
2 seconds
memory limit per test
512 megabytes
input
standard input
output
standard output

Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?

Every one of them has an integer sequences a and b of length n. Being given a query of the form of pair of integers (l, r), Mike can instantly tell the value of 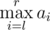while !Mike can instantly tell the value of .

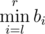Now suppose a robot (you!) asks them all possible different queries of pairs of integers (l, r) (1 ≤ l ≤ r ≤ n) (so he will make exactly n(n + 1) / 2 queries) and counts how many times their answers coincide, thus for how many pairs 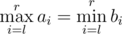is satisfied.

How many occasions will the robot count?

Input

The first line contains only integer n (1 ≤ n ≤ 200 000).

The second line contains n integer numbers a1, a2, ..., an ( - 109 ≤ ai ≤ 109) — the sequence a.

The third line contains n integer numbers b1, b2, ..., bn ( - 109 ≤ bi ≤ 109) — the sequence b.

Output

Print the only integer number — the number of occasions the robot will count, thus for how many pairs 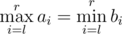is satisfied.

Examples
Input
6
1 2 3 2 1 4
6 7 1 2 3 2
Output
2
Input
3
3 3 3
1 1 1
Output
0
Note

The occasions in the first sample case are:

1.l = 4,r = 4 since max{2} = min{2}.

2.l = 4,r = 5 since max{2, 1} = min{2, 3}.

There are no occasions in the second sample case since Mike will answer 3 to any query pair, but !Mike will always answer 1.