| Codeforces Round 756 (Div. 3) |
|---|
| Finished |
You are given a rooted tree consisting of $$$n$$$ vertices. Vertices are numbered from $$$1$$$ to $$$n$$$. Any vertex can be the root of a tree.
A tree is a connected undirected graph without cycles. A rooted tree is a tree with a selected vertex, which is called the root.
The tree is specified by an array of ancestors $$$b$$$ containing $$$n$$$ numbers: $$$b_i$$$ is an ancestor of the vertex with the number $$$i$$$. The ancestor of a vertex $$$u$$$ is a vertex that is the next vertex on a simple path from $$$u$$$ to the root. For example, on the simple path from $$$5$$$ to $$$3$$$ (the root), the next vertex would be $$$1$$$, so the ancestor of $$$5$$$ is $$$1$$$.
The root has no ancestor, so for it, the value of $$$b_i$$$ is $$$i$$$ (the root is the only vertex for which $$$b_i=i$$$).
For example, if $$$n=5$$$ and $$$b=[3, 1, 3, 3, 1]$$$, then the tree looks like this.
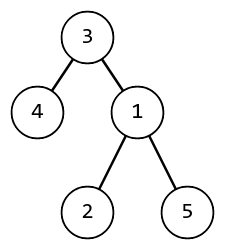 An example of a rooted tree for $$$n=5$$$, the root of the tree is a vertex number $$$3$$$.
An example of a rooted tree for $$$n=5$$$, the root of the tree is a vertex number $$$3$$$. You are given an array $$$p$$$ — a permutation of the vertices of the tree. If it is possible, assign any positive integer weights on the edges, so that the vertices sorted by distance from the root would form the given permutation $$$p$$$.
In other words, for a given permutation of vertices $$$p$$$, it is necessary to choose such edge weights so that the condition $$$dist[p_i]<dist[p_{i+1}]$$$ is true for each $$$i$$$ from $$$1$$$ to $$$n-1$$$. $$$dist[u]$$$ is a sum of the weights of the edges on the path from the root to $$$u$$$. In particular, $$$dist[u]=0$$$ if the vertex $$$u$$$ is the root of the tree.
For example, assume that $$$p=[3, 1, 2, 5, 4]$$$. In this case, the following edge weights satisfy this permutation:
- the edge ($$$3, 4$$$) has a weight of $$$102$$$;
- the edge ($$$3, 1$$$) has weight of $$$1$$$;
- the edge ($$$1, 2$$$) has a weight of $$$10$$$;
- the edge ($$$1, 5$$$) has a weight of $$$100$$$.
The array of distances from the root looks like: $$$dist=[1,11,0,102,101]$$$. The vertices sorted by increasing the distance from the root form the given permutation $$$p$$$.
Print the required edge weights or determine that there is no suitable way to assign weights. If there are several solutions, then print any of them.
The first line of input data contains an integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of input data sets in the test.
Each test case consists of three lines.
The first of them contains an integer $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$). It is the number of vertices in the tree.
The second line contains $$$n$$$ integers $$$b_1, b_2, \dots, b_n$$$ ($$$1 \le b_i \le n$$$). It is guaranteed that the $$$b$$$ array encodes some rooted tree.
The third line contains the given permutation $$$p$$$: $$$n$$$ of different integers $$$p_1, p_2, \dots, p_n$$$ ($$$1 \le p_i \le n$$$).
It is guaranteed that the sum of the values $$$n$$$ over all test cases in the test does not exceed $$$2 \cdot 10^5$$$.
For each set of input data print the answer on a separate line.
If the solution exists, print an array of $$$n$$$ integers $$$w_1, w_2, \dots, w_n$$$, where $$$w_i$$$ is the weight of the edge that leads from $$$b_i$$$ to $$$i$$$. For the root there is no such edge, so use the value $$$w_i=0$$$. For all other vertices, the values of $$$w_i$$$ must satisfy the inequality $$$1 \le w_i \le 10^9$$$. There can be equal numbers among $$$w_i$$$ values, but all sums of weights of edges from the root to vertices must be different and satisfy the given permutation.
If there are several solutions, output any of them.
If no solution exists, output -1.
4 5 3 1 3 3 1 3 1 2 5 4 3 1 1 2 3 1 2 7 1 1 2 3 4 5 6 1 2 3 4 5 6 7 6 4 4 4 4 1 1 4 2 1 5 6 3
1 10 0 102 100 -1 0 3 100 1 1 2 4 6 5 10 0 2 3
The first set of input data of the example is analyzed in the main part of the statement.
In the second set of input data of the example, it is impossible to assign the positive weights to obtain a given permutation of vertices.
| Name |
|---|




