| Codeforces Round 726 (Div. 2) |
|---|
| Finished |
You have a connected undirected graph made of $$$n$$$ nodes and $$$m$$$ edges. The $$$i$$$-th node has a value $$$v_i$$$ and a target value $$$t_i$$$.
In an operation, you can choose an edge $$$(i, j)$$$ and add $$$k$$$ to both $$$v_i$$$ and $$$v_j$$$, where $$$k$$$ can be any integer. In particular, $$$k$$$ can be negative.
Your task to determine if it is possible that by doing some finite number of operations (possibly zero), you can achieve for every node $$$i$$$, $$$v_i = t_i$$$.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$), the number of test cases. Then the test cases follow.
The first line of each test case contains two integers $$$n$$$, $$$m$$$ ($$$2 \leq n \leq 2\cdot 10^5$$$, $$$n-1\leq m\leq \min(2\cdot 10^5, \frac{n(n-1)}{2})$$$) — the number of nodes and edges respectively.
The second line contains $$$n$$$ integers $$$v_1\ldots, v_n$$$ ($$$-10^9 \leq v_i \leq 10^9$$$) — initial values of nodes.
The third line contains $$$n$$$ integers $$$t_1\ldots, t_n$$$ ($$$-10^9 \leq t_i \leq 10^9$$$) — target values of nodes.
Each of the next $$$m$$$ lines contains two integers $$$i$$$ and $$$j$$$ representing an edge between node $$$i$$$ and node $$$j$$$ ($$$1 \leq i, j \leq n$$$, $$$i\ne j$$$).
It is guaranteed that the graph is connected and there is at most one edge between the same pair of nodes.
It is guaranteed that the sum of $$$n$$$ over all testcases does not exceed $$$2 \cdot 10^5$$$ and the sum of $$$m$$$ over all testcases does not exceed $$$2 \cdot 10^5$$$.
For each test case, if it is possible for every node to reach its target after some number of operations, print "YES". Otherwise, print "NO".
2 4 4 5 1 2 -3 3 3 10 1 1 2 1 4 3 2 3 4 4 4 5 8 6 6 -3 1 15 4 1 2 1 4 3 2 3 4
YES NO
Here is a visualization of the first test case (the orange values denote the initial values and the blue ones the desired values):
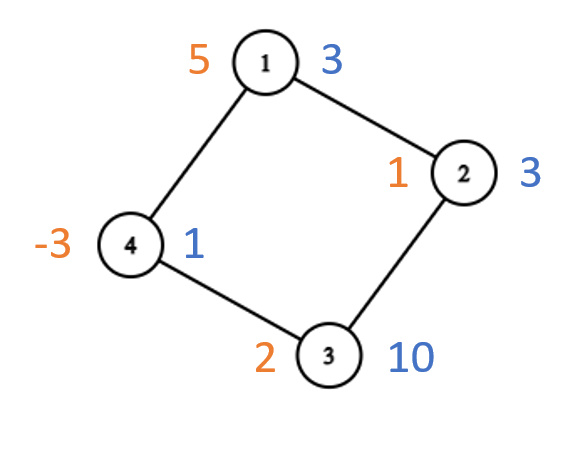
One possible order of operations to obtain the desired values for each node is the following:
- Operation $$$1$$$: Add $$$2$$$ to nodes $$$2$$$ and $$$3$$$.
- Operation $$$2$$$: Add $$$-2$$$ to nodes $$$1$$$ and $$$4$$$.
- Operation $$$3$$$: Add $$$6$$$ to nodes $$$3$$$ and $$$4$$$.
Now we can see that in total we added $$$-2$$$ to node $$$1$$$, $$$2$$$ to node $$$2$$$, $$$8$$$ to node $$$3$$$ and $$$4$$$ to node $$$4$$$ which brings each node exactly to it's desired value.
For the graph from the second test case it's impossible to get the target values.
| Name |
|---|




