A maze is represented by a tree (an undirected graph, where exactly one way exists between each pair of vertices). In the maze the entrance vertex and the exit vertex are chosen with some probability. The exit from the maze is sought by Deep First Search. If there are several possible ways to move, the move is chosen equiprobably. Consider the following pseudo-code:
DFS(x)
if x == exit vertex then
finish search
flag[x] <- TRUE
random shuffle the vertices' order in V(x) // here all permutations have equal probability to be chosen
for i <- 1 to length[V] do
if flag[V[i]] = FALSE then
count++;
DFS(y);
count++;
V(x) is the list vertices adjacent to x. The flag array is initially filled as FALSE. DFS initially starts with a parameter of an entrance vertex. When the search is finished, variable count will contain the number of moves.
Your task is to count the mathematical expectation of the number of moves one has to do to exit the maze.
The first line determines the number of vertices in the graph n (1 ≤ n ≤ 105). The next n - 1 lines contain pairs of integers ai and bi, which show the existence of an edge between ai and bi vertices (1 ≤ ai, bi ≤ n). It is guaranteed that the given graph is a tree.
Next n lines contain pairs of non-negative numbers xi and yi, which represent the probability of choosing the i-th vertex as an entrance and exit correspondingly. The probabilities to choose vertex i as an entrance and an exit equal 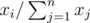 and
and 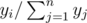 correspondingly. The sum of all xi and the sum of all yi are positive and do not exceed 106.
correspondingly. The sum of all xi and the sum of all yi are positive and do not exceed 106.
Print the expectation of the number of moves. The absolute or relative error should not exceed 10 - 9.
2
1 2
0 1
1 0
1.00000000000000000000
3
1 2
1 3
1 0
0 2
0 3
2.00000000000000000000
7
1 2
1 3
2 4
2 5
3 6
3 7
1 1
1 1
1 1
1 1
1 1
1 1
1 1
4.04081632653
In the first sample the entrance vertex is always 1 and the exit vertex is always 2.
In the second sample the entrance vertex is always 1 and the exit vertex with the probability of 2/5 will be 2 of with the probability if 3/5 will be 3. The mathematical expectations for the exit vertices 2 and 3 will be equal (symmetrical cases). During the first move one can go to the exit vertex with the probability of 0.5 or to go to a vertex that's not the exit vertex with the probability of 0.5. In the first case the number of moves equals 1, in the second one it equals 3. The total mathematical expectation is counted as 2 / 5 × (1 × 0.5 + 3 × 0.5) + 3 / 5 × (1 × 0.5 + 3 × 0.5)
| Name |
|---|




