В этой задаче требуется разделить все натуральные числа от 1 до n2 на n групп по n чисел в каждой так, чтобы суммы чисел во всех группах были одинаковыми.
Давайте разобьем все эти числа на пары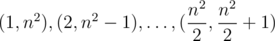 
. Это можно сделать благодаря тому, что n четное, а значит, и n2 тоже. Сумма каждой из этих пар равна n2 + 1. Теперь осталось только определить по 
пар в каждую из групп.
В этой задаче требуется сделать лишь то, что сказано — определить, удовлетворяет ли данный набор из восьми точек описанному условию.
Есть множество способов это сделать. Например, следующий:
Проверить, что среди координат этих точек есть ровно три различных x и ровно три различных y. Найти количество различных x (так же, как и y) можно, положив их в set и узнав его размер. Если оно не равно 3, вывести <>.
Итак, у нас есть x1, x2 и x3, а так же y1, y2 и y3. Осталось проверить, что для любой пары (xi, yj) (кроме (x2, y2)) данная точка присутствует среди восьми перечисленных. Можно просто перебрать все эти пары и для каждой пары, перебрав все восемь точек, выяснить, есть ли эта пара.
Однако я думаю, что читать решение в данном случае — неблагодарная затея. Лучше просто посмотреть реализацию.
334C - Секреты / 333A - Секреты
На самом деле, в задаче разыскивается самая длинная такая последовательность натуральных чисел a1, a2, ..., ak, такая, что каждое число в ней является степенью тройки, сумма всех чисел больше, чем n, и если выкинуть любое из чисел, то сумма станет меньше n. Если точнее, требуется лишь узнать длину этой последовательности.
Рассмотрим минимальное ai = A. Поскольку все эти числя являются степенями 3, то все остальные ai делятся на A и, следовательно, сумма всех этих чисел S тоже делится на A. Если n также делится на A, то, так как S > n, то S превосходит n как минимум на A. Следовательно, если выкинуть из последовательности число A, то остаток будет не меньше, чем n, а это противоречит второму условию. Таким образом, мы выяснили, что n не делится ни на одно из чисел этого последовательности, даже на самое маленькое. Тогда найдем минимальное k такое, что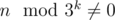 
— это легко сделать простым перебором. А дальше просто набрать минимальную сумму, превосходящую n монетами номинала 3k. Таким образом, ответом будет число 
.
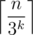В этой задаче требовалось найти максимальное количество фишек, которые Геральд может поставить на поле.
Сначала сделаем два замечания.
- На каждую линию (вертикаль или горизонталь) можно поставить только одну фишку, с одного конца или с другого.
- Если на линии есть хотя бы одна запрещенная клетка, то на нее нельзя поставить ни одной фишки.
Соблюдая последнее замечание, мы избегнем попадания фишек на запрещенные клетки. Осталось избежать <<столкновения>> фишек.
Рассмотрим следующие четыре линии: вертикали i и n + 1 - i и горизонтали с теми же номерами (i может быть любым, если только i ≠ n + 1 - i). Заметим, что фишки, поставленные на эти линии, могут столкнуться друг с другом, но не могут столкнуться с фишками на других линиях. Таким образом, для этих четырех линий можно решать задачу независимо от других линий. Осталось заметить, что мы можем поставить фишки на каждую из этих линий (на которой не стоит запрещенная клетка), так, чтобы они не столкнулись так, как это показано на картинке.
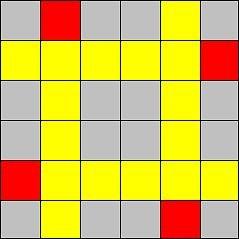
Итого, можно просто перебрать эти четверки линий и для каждой из них выяснить, сколько фишек можно на них поставить. И не забыть рассмотреть случай двух средних линий в случае нечётного n.
334E - Счастливые билеты / 333C - Счастливые билеты
В это задаче надо предъявить нужное количество счастливых билетов.
Давайте рассмотрим, сколько разных чисел можно получить таким образом из четырёхзначных номеров. Их легко перебрать, благо их всего 104. Оказывается, что в среднем получается почти 60 чисел на каждый четырёхзначный номер. Пусть из номера n можно получить число x. Ясно, что k - x ≥ 0 либо x - k ≥ 0. Если, например, k - x ≥ 0, мы можем записать восьмизначный номер, в первых четырех цифрах которого будет записано k - x, а в последних четырех — n. Понятно, что такой билет будет k-счастливым. Всего это дает нам почти 600 000 билетов, этого вполне достаточно.
333D - Характеристики прямоугольников
По сути, в этой задаче надо найти, каким наибольшим может быть значение минимума из четырех клеток на пересечении двух столбцов и двух строк.
Иными словами, надо найти максимальное значение величины min(ai1, j1, ai1, j2, ai2, j1, ai2, j2) при всех i1, i2, j1, j2 таких, что 1 ≤ i1, i2 ≤ n, 1 ≤ j1, j2 ≤ m, i1 ≠ i2, j1 ≠ j2. Давайте применим бинарный поиск по ответу. Для этого надо научиться находить, есть ли в таблице из 0 и 1 два столбца и две строки, на всех четырех пересечениях которых стоят единицы, то есть, такие i1, i2, j1, j2, что ai1, j1 = ai1, j2 = ai2, j1 = ai2, j2 = 1. Давайте рассмотрим все такие пары натуральных чисел (i1, i2), что существует натуральное число j такое, что ai1, j = ai2, j = 1. Наличие двух одинаковых таких пар как раз и означало бы наличие вышеописанных четырех чисел. Однако, всего может быть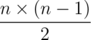 
таких пар. Следовательно, мы можем завести массив, где будем отмечать, какие пары уже встретились и перебирать все пары в любом порядке, пока не встретится повторяющаяся пара или пока все пары не будут перебраны. Итого, получаем решение за время 
.
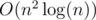В этой задаче требуется нарисовать три непересекающихся круга максимального радиуса с центрами в заданных точках. Иными словами, нам надо найти треугольник у которого минимальная из сторон будет максимальна.
К сожалению, мы не ожидали решения с битовой оптимизацией, которое оказалось для участников проще нашего.
Вспомним факт из школьного курса геометрии, говорящий, что напротив большего угла лежит большая сторона. Кроме того, вспомним, что сумма углов в треугольнике равна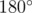 
. Из этого следует, во-первых, что как минимум один угол в треугольнике не меньше 
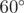. Во-вторых, что этот угол не может быть самым маленьким в треугольнике. И следовательно, что напротив этого угла лежит не самая маленькая сторона. Следовательно, если в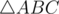 
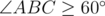, то min(|AB|, |BC|, |CA|) = min(|AB|, |BC|).
Следовательно, мы можем поступить следующим образом. Переберем вершину B и найдем треугольник с максимальной минимальной стороной среди таких, у которых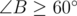 
. Для этого отсортируем все остальные вершины по углу относительно B, и для каждой вершины A найдем самую удалённую от B вершину C среди отрезка тех вершин, для которых 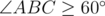. Для этого нам понадобится использовать дерево отрезков для максимума и два указателя или бинарный поиск, чтобы хранить левую и правую границу возможных вершин C при переборе вершины A.
Итого, получаем решение за время .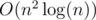
Третья задача — очень туго написано условие, я так и не понял, что нужно самую длинную последовательность: "чем надо сумму как можно меньшим количеством монет. Какое максимальное количество монет у него могло получиться?"
С одной стороны: как можно меньшим количеством монет, а с другой Какое максимальное количество монет у него могло получиться?
Помогите, пожалуйста, найти ошибку в 333C - Счастливые билеты? Решение такое же, как в разборе 4186556, на домашнем компе работает, а на сервере переменные не хотят быть отрицательными при вычитании бОльших чисел...
Вы обратили внимание, что в тесте просят три билетика, а Вы выводите много и большинство из них 12значные, хотя должны быть 8значные?
Конечно же да. На домашнем компе или на сервере с компилятором MSC++ 4185456 выводится 3 билетика, но там дальше возникают проблемы, теперь уже в 3-м тесте. UPD: Все, спасибо, мне помогли — проблемы была в обращении к массиву с отрицательными индексами.
У меня в Е решение тоже за O(N2·logN), но как по мне — оно более простое.
Сделаем бинарный поиск по ответу r. После этого, переберем одну точку. Рассмотрим набор всех точек, которые отстоят от нее хотя бы на 2r. Если в этом множестве 2 самые удаленные точки лежат на расстоянии хотя бы 2r, то радиус r нам подходит, иначе — нет. Найти 2 самые удаленные точки можно за линейное время, при условии что мы уже построили их выпуклую оболочку. Заметим, что если мы предварительно отсортируем все точки по иксу, то выпуклую оболочку можно также построить за линейное время.
Интересно, спасибо.
Не сказал бы, что это более простое решение, по-моему, примерно такое же по сложности. В моё решении, хотя главная идея (про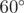
) более нетривиальная, но после неё сразу понятно, что делать.
Написал тоже самое на джаве на контесте получил ТЛ :( В дорешке переписал на плюсы — зашло...
Мне почему-то кажется, что если не извлекать корни в самом глубоком месте программы, время работы будет намного меньше.
Я пробовал предподсчитать все расстояния вначале программы и это работает еще дольше.
Можно вообще нигде корни не извлекать, а оперировать с квадратами. Мое решение, когда я стал делать 33 итерации бинпоиска вместо 85, стало работать 1.5с. Мне кажется, если переписать его на Java, то оно тоже должно пройти, ТЛ ведь аж 9 секунд.
Может я действительно слишком неаккуратно пишу. Попробую избавиться от корней...
А как строить выпуклую оболочку, если точки отсортированы по иксу?
Graham
Если не учитывать сортировку, то все делается за О(n).
Div1 B сначала решал без учета того факта, что матрица квадратная. Ее вообще можно решить для произвольного прямоугольника? Если не для таких ограничений, то хоть как-то быстрее перебора битмасок?
У меня были какие-то мысли о потоках, но придумать не получилось.
Наверное, можно найти наибольшее независимое множество в графе, где вершины -- это граничные (но не угловые) клетки, и если поставить в две различные клетки по фишке, то если, они будут конфликтовать (т.е. пути фишек из этих клеток пересекаются), то ребро между соответствующими вершинами есть, иначе нет.
UPD: Хотя, фиг его знает, какая там асимптотика.
Есть идея подсчитать для каждой фишки количество конфликтующих с ней фишек — то есть таких, которые нельзя будет поставить, если будет поставлена рассматриваемая фишка (таких вначале максимум 3, минимум 1).
И после этого ставим фишки, пока можем. На каждом шаге выбираем фишку с минимальным кол-вом конфликтующих. Если таких несколько — ставим любую. Поставив фишку, помечаем конфликтующие с ней, что их уже тоже нельзя ставить и пересчитываем (уменьшаем) кол-во конфликтующих для "задетых" в результате этих манипуляций фишек.
Не могу доказать формальнее, как это работает, и работает ли вообще, но такое зашло на контесте, поэтому я подумал, что может сработать и для прямоугольной матрицы.
У меня такое не зашло на контесте.
I believe it's
O(n^2 log max(a))in DYou can sort all values of our table and do binary search on this sorted sequence, which leads to O(N2·logN) algo
OK, sure.
It's O(n^2log(n^2))
O(log n^2) = O(2 log n) = O(log n)
Use binary search over a sorted list of existing numbers from the table instead of an entire range [1,10^9]. This gives you O(log(n^2)) = O(log(n)) as mentioned in the editorial.
Yes — this turned out to be crucial in accepting my bitset-bruteforce in D :)
can you tell me what is "bitset-bruteforce" solution?
You can look at my code.
how many times bitset array faster than bool array?
Around 32.
Using bitset in C++ STL, we can pass D and E :(
Using bitset in C++ STL, we can pass D and E :(
please can you write some details for these solutions
If we want to pass E An algorithm O(n^3):for circle i,j,k,we can check it and get answer. We know all distance of every pair,sort it If dis(i,j) is answer,dis(i,k)<=dis(i,j),mark[i][j]=true.I try each answer and they are sorted,so when I try dis(i,j),if mark[i][k]=true and mark[j][k]=true,we can print dis(i,j) If mark[i] is a bitset,and the k is exist,then (mark[i]&mark[j]).any() is not 0. We have an algorithm,O(n^3/32),and it can pass E Sorry for my English.In fact,my English is so poor that my teacher criticized me. T_T
Another way to solve E: first, binary search on the result r (complexity factor: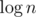
), then fix one vertex A of the triangle (complexity factor: n). We want to find two other vertices B, C such that all three distances are ≥ 2r. Let's consider only the set S of those vertices that are farther than 2r from A. Now obviously, there are two vertices 
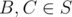with dist(B, C) ≥ 2r if and only if the maximum distance of two points in S is ≥ 2r. And this can be found using convex hull and rotating calipers (complexity factor: 
).
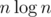(Actually, we need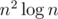
, not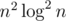 
. But notice that the 
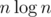in convex hull comes from sorting the points. We can do that just once after reading the input. Then, after filtering out the too-close vertices, the list is still sorted.)
Very nice solution.
I tried to implement it on my own. I just want to add, that it must be implement very carefully. It's important to avoid using double arithmetic, because you can recieve TLE. But with long longs, it's fast enough.
I changed one line in your solution (4195968) and it became two times faster :)
Of course, I should realize, that I don't need long longs. And arithmetic on ints is even quicker. Thank you, for your tip :)
for problem Div1 D ,How this submission with complexity O(N^3) passed? 4183580
also how functions fastMax and fastMin work?
it is really surprising, i replaced min/max by fastMin/fastMax and it got accepted!!! (time taken = 2.9s)
-1 & (x ^ y) = (x ^ y).
(x ^ y) ^ y = x.
0 & (x ^ y) = 0.
0 ^ y = y.
deleted
Wow, nice :D. How many times approximately is this fastMin faster than the usual one?
Besides, I think that finding such formulas for min and max is much harder than that problem :P.
How does operators
<<and>>work for negative numbers?Implementation defined as I remember.
Usually it's multiplication/division by 2 (rounding down)
I did some tests.
rep(i, 1000000000) a = std::max(1000, -1000);takes 4148.88 ms
rep(i, 1000000000) a = fastmax(1000, -1000);takes 3738.1 ms
It's near 10% faster; not that great. Asymptotic running time is still the big deal. Having this trick under your sleeve is nice though.
PS: With any optimization flag they both take 0 ms :P
you can't test in this way. because iterating from 1 to 1000000000 the jump operations and add operations spent most of the time.
try like this: rep(i, 1000000) { a = fastmax(1000, -1000); a = fastmax(1000, -1000); a = fastmax(1000, -1000); a = fastmax(1000, -1000); ... ... 1000 times ... a = fastmax(1000, -1000); }
Am I the only one who got accepted without any fastmax and fastmin ? 25100623 My O(n ^ 3) solution passed comfortably in 2 seconds
334C — SECRETS
for n=8 ... can not the buyer just give 9 mark coin ??
May be, he haven't this coin?
I'm surely missing something here .. , because I don't get the point of buyer not having 9 mark coin (as it is given that buyers have all the denominations that are divisble by 3), pls hlp!!! this question is really confusing me
yes, he can, but this is not the maximum number of coins. the maximum number is 3 (3 mark coin);
pls explain this -> For each such combination calculate the minimum number of coins that can bring the buyer at least n marks
{ for n=8 :
9-> 3+3+3 (it can not be further reduced) or 9
10->not possible
12-> 3+3+3+3 reduced to 3+9 ... } Is above explanation of mine is correct??
No, it is not correct. the problem statement says " Among all combinations choose the maximum of the minimum number of coins "
Sorry for posting here so late: The combination are: For 9: it's 1 (denomination 9) For 10: it's 2 (9+1) For 12: it's 2 (9+3) . . Till which mark do we need to iterate and for 8 how the answer is 3. Kindly clarify them. TIA.
I can't understand D's solution. Can anybody explain more clearly?
Nobody care
Care cái sỏi
I am finding it difficult to understand the solution of D too.
We binary search for the answer. Note that the answer is one of a[i][j] only. So for a fixed k, we want to find whether there exists a rectangle all 4 of whose corner numbers are >= k. So to do this for a fixed k, define a boolean array b[n][m] where b[i][j] = 1 if a[i][j] >= k and 0 otherwise.
Now the problem is reduced to finding a rectangle in b[n][m] all of whose corner numbers are 1. For each pair of rows (r1, r2), if there exists a j such that b[r1][j] = b[r2][j] = 1 then we say that (r1, r2) is a "good" pair. Note that there are atmost nC2 good pairs. Now we iterate over all pairs of 1's that are in the same column, and mark the pair of corresponding rows as good (in a map). If the pair is already present in the map, "k" can be obtained and we are done. Keep iterating in any random order, till you encounter a repeated good pair of rows. If you exhaust all vertical pairs of 1's and still don't have a repeated good pair of rows, then "k" cannot be obtained and we are done again.
Won't iterating over all pairs of 1s that are in the same column be O(n*n*n)?
Store an array good[n][m] initialized to 0.
Now, for each row: Store positions of all 1s in a vector
For each pair (i,j) in the vector:
If good[i][j] is 0, set good[i][j] to 1.
If good[i][j] is 1, then that means there exists a column in which row i and row j are set to 1. And in the current column, row i and row i have values 1 as well. Therefore, we have our answer and stop here.
So, initially all of good[n][m] is 0. At each step, you are changing a good[i][j] to 1. You can only do that N*N times. When you find you are trying to change a good[i][j] that is already 1, you stop.
You are so cute when rehearsing the content of this post =)
Is that sarcasm?
hm, and judging by amount of downvotes few understood it...
So you mean good[m][m] not good[n][m]... right?
That one was confusing me.
Thank you guys, now I understand the solution. The tutorial says that we must find a rectangle with 4 of its cornors are 1, and I really don't know what the heck 1 is =))
for problem Div1 D ,will it take o(n) to find j so that ai1,j= ai2,j=1? when we meet repeated pair and return(4183297),how to compute the overall solution of time,why it's o(n^2 log(n))?
Though it seems has O(N^3) iterations to find the two pairs, in every iteration it will find a new good pair(record it in a 2-d array good) or a repeated pair(thus find the two pairs and return). There are only O(N^2) states in 2-d array good, So it has at most O(N^2) iterations overall. Combined with binary search of answer, it gives O(N^2)log(n) algorithm. Codes 4192623
I am very annoyed by the bad translation !
Добрый вечер! Задача про "продажу секретов", условие некорректно. Согласно условию надо найти минимальное количество монет, которым можно собрать сумму выше требуемой. Ответ удовлетворяющий всем условиям задачи один для любых требуемых сумм, а именно 1 (одна) монета. С помощью одной монеты достоинством степень тройки выше требуемой суммы можно выплатить сумму большую требуемой. Причем в разборе еще указано одно условие, которого в задаче нет : типа если выкинуть монету, то сумма станет меньшей требуемой. Но даже в этом случае решение "одна моента" удовлетворяет этому условию, уберите ее, и сумма станет нулевой (что естественно меньше требуемой)
Мы берем максимум по всем возможным конфигруациям таким, что ...
Наличие комбинации с ответом 1 ничего не значит.
Все возможные комбинации с суммой выше требуемой? Причем с целью уменьшить число монет? Предположим (условно) требуется сумма 90 мы можем выдать сумму 3^100, выше она требуемой? да, число монет минимально — да (одна монета). но мы можем выдать и монеты подругому. но в этом случае будет нарушена цель плательщика (выдать минимум монет) или я что то пропустил? Хорошо можно зайти с другой стороны, найти максимальное число монет, если включить в условие задачи требование "если выкинуть любую монету из набора, то сумма станет меньше требуемой" и убрать минимизацию со строны плательщика... но в условии есть минимизация но нет условия "выкинуть..."
Так-так-так-так-так. Давайте-ка прочитаем условие. "Тогда он постарался из имеющихся у него монет выдать Геральду большую, чем надо сумму как можно меньшим количеством монет". Из имеющихся у него монет. Он может выдать сумму больше, чем надо, одной монетой, только если она у него есть. А если, скажем, у него только монеты номиналом 27 и 81? Тогда ему придётся выдать две монеты 81 + 27 или 81 + 81. А в каких-то случаях ему придётся использовать ещё больше монет. Вот и спрашивается, какое максимальное количество монет ему придётся использовать.
На самом деле условие действительно мутноватое. Но там еще есть последний абзац, который все объясняет.
Спасибо за контест)
В условии задачи нет данных, которые указывали, какие монеты есть, а каких нет. Из этого следует что у его есть любые монеты. Максимальное число монет, которой можно выдать сумму больше нужной равно бесконечности, поскольку ограничения на сумму накладываются. Например при цене секрета в 1 марку, что в условиях задачи мешает заплатить миллион? А десять? А сто? Так что минимум набора — одна монета, максимум — бесконечность...
На самом деле рассуждал ровно также во время контеста. Но предлагается рассмотреть все возможны комбинации, в которых нельзя дать точно N марок. Для каждой такой комбинации выпишем минимальное число монет, которым можно расплатиться. Среди всех таких выписанных нужно выбрать максимальное число (это деобфусцированная последняя фраза условия)
На самом деле ты бы мог позадалбывать вопросами жюри, как сделал я, и понять условие.
Во-первых, это продолжение естественной ситуации, которая была описана в условии — к Геральду приходит человек, чтобы купить секрет, у него в кармане есть какие-то деньги, но не все деньги государства, конечно. Именно поэтому вполне может оказаться, что у него не найдётся нужная сумма без сдачи. Если не опираться на ситуацию, описанную в условии — то зачем она вообще? Дали бы сухую математическую формулировку. Можно было и так сделать, но раз дали живую легенду, то не просто так, а для того, чтобы опираться на неё при понимании условия.
Во-вторых, написано же — " из имеющихся у него монет". Это ясно указывает, что речь идёт не он всевозможных монетах, а только о тех, которые у него есть. А раз об этом идёт речь — значит, это не одно и то же.
В третьих, да, в условии нет данных, которые указывали, какие монеты есть, а каких — нет. Но это указывает не на то, что него есть любые монеты, а на то, что у него любые монеты могут быть, с таким же успехом, как и не быть.
Неправда ваша, перечитайте условие.
Can someone please explain the logic behind Div2 C problem ? I am not able to understand the tutorial.
Ok. We see from statement, that we are looking for the longest possible sequence a1, a2... ak with these properties:
all numbers ai are powers of three -- we only know coins with these values
sum S of these numbers is larger than n -- we must pay larger amount of marks, because buyer doesn't have exact amount
Now denote minimal ai as A. Other ai are larger or equal, so these number are multiples of A. If S is sum of all elements ai and each element is divided by A, than S is also diveded by A.
Now let's consider, that n is diveded by A. We know, that S is multiple of A, n is multiple of A and S is larger than n. So S - n ≥ A which means, that n ≥ S - A. But this is contradiction with last property of our sequence. So n cannot be divided by minimal ai in our sequence.
Last thing is, that if we want the longest sequence, all numbers should be equal. This is pretty obvious, because if A is minimal element, than any larger element is multiple of A and can be distributed to more A elements.
Now you can iterate through all k such as 3k ≤ n. If 3k doesn't divided n, than you can obtain answer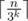
. And the biggest such number is final answer. If n is power of three, then answer is 1.
My code here: 4175901
I hope, this will help.
Thanks for a great explanation :)
I've got similar solution for problem Div1-D, but I don't use binary search. Complexity of my solution is still
, but in my opinion it's easier to implement.
So the main idea is the same. Consider pair of columns (c1, c2). Two such pairs in different rows (r1, r2) creates one possible solution -- rectangle with characteristic min(ar1, c1, ar2, c1, ar1, c2, ar2, c2). And we want the largest characteristic.
We sort all numbers in rectangle from the biggest to the smallest. Now we will add these number in this order. When we add element ai, j it creates pair of columns with every element on row i, which are greater (or equal and were added before). So we store these elements in vector (one for each row) and iterate them. During this we count, how many times we see which pair of columns. When we see some pair the second time, we have possible solution and because we add elements from biggest one, it's also the largest rectangle. So value of the last added element is answer.
Time complexity: we need time
time for sort all numbers. Then we add each pair of columns at most once, so the complexity is O(n2). Overall it's 
.
Here is my code: 4183958
Поясните, пожалуйста, решение задачи Div1 D. Никак не могу понять, как за квадрат можно проверить существование двух одинаковых пар (i1,i2) и двух различных j, им соответствующих. Больше всего не понимаю фразу "перебирать пары в любом порядке, пока не встретится повтор". Кроме того, в моем понимании, наличие двух одинаковых пар (i1,i2) не говорит о наличии четырех единиц в углах: j может быть одинаковое у них.
Для каждой строки выпишем все номера стобиков, в которых находятся числа, большие либо равные текущему значению, которое мы перебираем бинпоиском. В лоб переберем все пары таких столбиков. Если такая пара когда либо встречалась — то это однозначно происходило в одной из прошлых строк. Если такое повторение есть — прямоугольник существует. Иначе же, мы переберем не более O(N2) пар, потому что их всего O(N2)
I'm sorry but after reading this editorial I'd a feeling like this
in my opinion:
RIP codeforces editorials
Learn a lot from your solution of 333E - Летний заработок. thx. :D
Кто знает подскажите пожалуйста. Задача "Счастливые билеты" ошибка wrong answer Line [name=current number] equals to "", doesn't correspond to pattern "[0-9]{8,8}" на тесте 15, но все ответы совпадают с шаблоном, в каких ещё случаях эта ошибка может вылетать?
Такая ошибка означает всего лишь, что Вы где-то вывели пустую строку, причём до неё не оказалось нужного количества билетов.
In E, we can avoid implementing segment tree and use a deque to maintain maximum on interval that is being held by two pointers (check this submission 4213091).