→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
16:22:46
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
16:22:46
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/30/2024 01:12:15 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Sorry if this question has been asked before, but I quickly Googled it just now and can't find it.
Is there a way to change our COCI account password? Thanks.
Step 1: Go to http://evaluator.hsin.hr/login.php?redirect=index.php
Step 2: Look at the line "Forgot username and password..." and you will see a link directed to an other website.
Step 3: Enter your email you used to register.
I didn't try, but I hope these will help you.
I just tried this. This feature will generate a new (random) password for you and the new password will be emailed to you.
I want to be able to change it to my own custom password.
There is currently no feature that allows you to change your old password to a custom one, sorry.
try to send clarification request
duration ?
Three hours.
Good luck to everyone!
Weird. I don't see tasks.
Is there something with 0, (2^m)-1 and subsequence that xor of all elements == (2^m)-1 in E task?
How to solve C, E, F?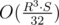 for C?
for C?
Is there smth faster than
E: An interval can't win iff it contains exactly 2k pair (x, 2n - 1 - x).
Do you have any proof?
Proof is easy. Let its xor sum be X. Then for each element a in that interval we must have a^(2n - 1)^X also is in that interval. So we have d pairs (a, a^(2n - 1)^X). Because its xor sum is X, so X must be 0.
How do you check if an interval meets the condition effectively?
Denote N = 2M - 1.
You can answer the queries of the type "maximum/minimum index i such that N - perm[i] exists in the target interval" in O(1) with O(NlogN) or even O(N) precomputation with RMQ. Then, if the answer to any of the queries doesn't belong to the target interval, the interval is winnable (as explained in chemthan's post).
Unfortunately, as the task is to count the winnable intervals rather than answer to queries, this method is only O(N2), which is enough only for 50% of the points.
How to solve it after this? It seems now it reduces to: count the number of subarrays with exactly 0 or 2 instances of every element.
If my solution is correct, time complexity of my solution is O(R2 * S)
Problem C
Yeah, that was the intended solution.
So can you explain it?
Sure, let's first think about the game in a different light. Suppose that everything on the grid stays still and the main character can in one second move from (r, c) to (r - 1, c - 1), (r - 1, c) or (r - 1, c + 1). It is easy to see those games are equivalent.
Let dp[r][c][o] denote the longest valid expression you can acquire if you are currently on position (r, c) on the screen and the difference between the number of open parentheses and closed parentheses in the expression you have acquired thus far equals o. Computing all dp values takes O(R3) time. This solves the part of the problem that deals with the length of the sequence.
For the reconstruction, we'll keep around a set of dp states that can potentially lead us to the lexicographically smallest solution. At the beginning, that set contains only Mirko's initial position. We will now make transitions from those states (similar to transitions in dp) that lead to longest solutions and traverse only the empty cells of the grid (this is a standard bfs). Once we have exhausted the empty cells, we have obtained the set of cells that contain the next parenthesis in our sequence. At this point we will disregard all cells that have ')' written on them in case there exists a single cell with '(' written on it. Repeating this process yields the lexicographically smallest sequence in O(R2).
Since there is no test case with expression longer than 50, separate reconstruction part is actually not needed. We can define dp value as pair of (longest valid expression, lexicographic price of expression) and then just maximize this pair using dp.
If for some state longest valid expression is k then lexicographic price is k-bit number created from this expression with
(being 1 and)being 0 — this k-bit number is solution itself.EDIT: Actually I modified this approach a bit and it works for all possible cases i.e. with expressions up to 100, just replace k-bit number with solution string, add custom operator< and then just print that string at the end.
What makes you think there is no test case with expression longer than 50?
Well, I meant in this specific contest there was not :). Of course there could be a test case with expression longer than 50.
You made me a bit paranoid for a second because I generated the test data :)
Now I see that we uploaded the wrong .zip archive at hsin.hr/coci which contains the test data for our local version of the contest (honi). That version of the task had looser constraints and the solution you described was supposed to get accepted.
The correct archive should be up tomorrow.
As noted in the edit of my comment above, this approach is working for all possible test cases if the lexicographic price part is replaced by plain string, bitset could be used as well. Thus special reconstruction phase could be avoidable after all. Waiting for additional test cases.
Wasn't C was harder than other C's in COCI?
Yes, considerably.
D is pretty easy right? Unless I missed something that made it hard...
Yeah.. Did you wrote simple BFS like me?
Same here. Honestly, C and D should be swapped.
Im not sure simple bfs was the optimal way. My code was not that simple
oh my god! I didn't read the D ,because i wanted to write c with recursion. #facepalm
really ,it is a simple bfs.
Yup. Well two BFS, but still very simple. I actually have a stupid typo in my last submission so it won't pass but it definitely seems too easy.
I don't know, but it reminded me this problem: http://codeforces.me/contest/877/problem/D
Do you know when can i see the results?
Usually, after 40 min. we can see results, but there can be delay sometimes.
Results delayed :(
in messages i saw this " Results will be available tomorrow. Thank you for patience. "
What is the optimal solution in problem B?
Precalculate prefix sums for each letter. When answering queries, check if count of each letter in same on intervals.
What is the solution for C? I wrote a solution that works in O(3^R), but it is obviously too slow.
Will they open the analysis mode?
Turn on analysis mode please.
The analysis mode is open now.