Let's discuss problems.
How to solve 2, 3, 6, 7, 11?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
Let's discuss problems.
How to solve 2, 3, 6, 7, 11?
| Название |
|---|



And 4, please :)
dp[L][R]= cost to join stations of interval [L, R] at point (x[L], y[R]).Calculate it as min value
dp[L][K] + dp[K+1][R] + (x[K+1] - x[L]) + (y[K] - y[R]).Answer is dp[0][n-1] + path from (x[0], y[n - 1]) to (0, 0)
Hey-ho, the contest is still running!
9 ?
You need to find the number of primes (let P be a prime)
2 <= P <= 10^7such that N is the smallest number soQ ^ N % P = 1From Fermat's little theorem,
Q^(P - 1) % P = 1, since P is prime, so N < P.Also, since
Q ^ N % P = 1Q ^ (2 * N) % P = 1andQ ^ (P - 1) % P = 1we know that N is a divisor of P — 1If N is not the smallest number so
Q^N % P = 1, there must be a number D, so D is a divisor of N (like N is a divisor of P — 1)For each divisor of N, D, check if
Q ^ D % P = 1, if that's true, N is not the first number that respects the property.If N is ok and all divisors fail, P is part of the solution for N
One can only check divisors of the form , where p is prime divisor of N
, where p is prime divisor of N
You can also check a divisor if it'a both a divisor of both N and P - 1
In fact, you can get a very fast O(T) solution (T = 107) without even doing fast exponentiation (after you precalc primes, of course).
Since you search only primes P = k * N + 1, there are only T / N candidates. So you can check each of them in O(N) time with trivial exponentiation, i.e. take 1 and multiply it N times.
Is 6 like a typical "Write the most lazy segment tree you can"?
I think you can solve 6 with cascading on segment tree. You also must keep a strange thing in each node. For the lazy part, on each node it will amortize at the end at O(number of els on that node)
the lazy part is like: "Ok, so on this node every value bigger than X will become X". When doing updates on first array, some values may become less than X. You will keep how many values are bigger than X and the product of elements lower than X.
The way I implement lazy is like this: If you pass throw a node, you propagate the lazy to the children and the current node has no lazy. Here, every node will have a X value, and when propagating the lazy, the value X will only increase, so the overall complexity will be O(sizeofnode)
The lazy part comes from how you compute an array c[i] = max(initial_swag, b[1] .. b[i — 1])
I didn't implement this, but it seems good. O(NlogN) time and memory.
Don't know if this will help, but it's the last line of the input. It's the only place where i saw this information
"It is guaranteed that with each change the older parameter value is strictly smaller than the new value."Not only
"Each change either raises ... or raises ....". Raising means increasing7
Mx regex size if 16
((a|(c|(g|t)))*)which matches anything.Can you do better than using regex implementation for every string?
PS: this gets TLE
This is the indended solution: check each regex of length < 16 against all strings.
However, your success largely depends on how many candidate regexes you have (there are various ways to prune regexes), and how you check a string against a regex (again, a lot of options here).
I had around 110K regexes, Which is a lot.
Also, is C++'s std::regex_match enough to pass the test-data?
Java's java.util.Pattern is enough, but std::regex is very slow.
In this article, std::regex_match has exponential time complexity. In this problem,
(((a*)*)t)andaa..aagtakes extremely long time.I don't know std::regex_match could get AC, but it must be used carefully.
These sometimes called "evil" regular expressions. Some examples of slow working regexes constructions to avoid are given here.
I'm pretty sure that std::regex was not enough while java Pattern was enough. Meet the problem where C++ library sucks, while Java library works =) The right way to match regexes is to build nondeterministic automaton.
Also, it is rather easy to decrease number of regexes to 40K by removing 0, pruning closing or "or"-ing a closure, ensuring A < B for (A|B), and removing cases like (A(BC)) in favor of ((AB)C).
Was interested in this problem and solved it in around a week.
Used to generate all possible regexes, excluding "duplicates" and longer equivalents if there are shorter ones. Got TLE.
Here are some ideas which I used to get AC:
Found minimal number of Kleene stars regex can contain.
Found minimal cardinality of sets consisting of different letters, otherwise regex
/[<set>]*/(in Simon's form) can be used as the shortest one.Later used "abstract" regular expressions consisted of dots (dot = match any letter). Earlier algorithm generated only few hundreds of such regexes. So an input data meets only some hundred "abstract" regular expressions, and often only some decades of them survive. Later I feed "abstract" regex with permutated letters and got some thousand normal regexes. This increased a speed or program significantly and still brought TLE.
Finally, remembered that one should pre-compile all regexes (
qroperator) before use them against plenty of test sets, otherwise they compile each time. Got AC 2.5s.Perl code.
Link to the problems?
How to solve 8?
Lets make a list c so that c[i]=a[i]-d[i].
for any [l,r], you need to make (r-l+1)/3 players with the lowest c forwards, (r-l+1)/3 with the highest c defenders, and other (r-l+1)/3 midfielders.
It can be easily done with persistent segment tree in O(q*logn*logn).
Isn't it an overkill? Binary indexed tree + parallel binary search is enough.
Could you please describe how parallel binary search works?
http://codeforces.me/blog/entry/45578
can you please elaborate on your persistent segment tree?
We want to find k-th smallest ellement in [l,r] segment. We construct Persistent tree with values c[i]. Then We use binary search for know index k-th minimum element and for checking this we use persistent tree. code https://ideone.com/bk5Qag
There is also a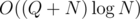 solution, although implementing it during the contest was probably not the best idea.
solution, although implementing it during the contest was probably not the best idea.
Define value of player to be difference of his attack and defense. Now sort players by value (and by index in case of ties). From this point build a segment tree on them, and in each node of the tree store all its players sorted by index, and prefix sums of their values alongside.
Now you can perform queries like "how many players with indices in [L..R) have values in [Vmin..Vmax)" in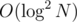 time using standard segment tree operation (you have to run binary search by L and R in each node of the tree). So you can use another bin.search to find values V1 and V2, such that the number of players with indices [L..R) is equal for the value ranges [Vmin..V1), [V1..V2), [V2..Vmax). You can use prefix sums to find sum of values in each of the value ranges, so this gives
time using standard segment tree operation (you have to run binary search by L and R in each node of the tree). So you can use another bin.search to find values V1 and V2, such that the number of players with indices [L..R) is equal for the value ranges [Vmin..V1), [V1..V2), [V2..Vmax). You can use prefix sums to find sum of values in each of the value ranges, so this gives 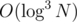 per query solution.
per query solution.
Now recall that in a standard RSQ segment tree we can do operation like "which maximal prefix of array has sum less than X" in time, which is better that doing binary search by position and calculating sum on prefix inside (which is
time, which is better that doing binary search by position and calculating sum on prefix inside (which is 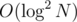 ). Now apply this idea to the segment tree above, and you don't need the outer binary search by value. So the solution becomes
). Now apply this idea to the segment tree above, and you don't need the outer binary search by value. So the solution becomes 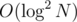 per query.
per query.
Finally, you can use fractional cascading to avoid running binary search by L and R in each node, so that you need only one binary search at the root node. This gives per query solution.
per query solution.
There is a similar/equivalent solution with Wavelet trees.
Just modify the k-th element function with some prefix-sums to return the sum of the k smallest elements instead.
2: Keep going forward. At the right moment turn right. Keep going forward again. At the right moment stop and dig.
When you keep going forward, you get a sequence of 'c' (closer) and 'f' (farther or same). If you analyze various patterns, you can notice that the run lengths of this sequence has a period of 8. You should stop when you just get 'c', you expect to get 'f' next, and the run length of current 'c' is maximum possible.
I haven't solve (fail on TC #2) and tried another approach: go forward if answer was "c", otherwise go random to L or R, until you stay in a cell from which you can get only "f" answer for all 4 directions. This means that you stay in correct cell, or in cell which is in mirror side of the cube. Then you go 1 circle around cube with two stops at c/f boundary, and dig depending on lengths of last "f" and "c" sequences.
I solved with same approach
11?
Binary search over answer. Let's check the distance
d, i.e. check ifnsegments is enough. It should be obvious that the greedy strategy should work, i.e. each segment should be as long as possible. Easy to see, that the best way to approximate some interval[x0, x1]is a line that passes through the points(x0, f(x0) + d),(x1, f(x1) + d ), let's say it's a liney = kx + b, then the maximum distance tof(x)will be at point withx = c / kor at the ends of the segment. So we can use one more binary search to find the maximum length of each segment, and build them one by one.There is a solution of O(1).
3?
I tried to access these problems on yandex but it said I need "coordinator login & pass".
How can I look at these problems?
We make this cube to solve 2 in contest, and this is very helpful.