Given two integers N and M, count the number of integers x between 2 and N! , having the property that all prime factors of x are greater than M. Where 1≤M≤N<10000001 and (N-M)≤100000. Can anyone help me with the logic?
→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
15:29:15
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
15:29:15
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/30/2024 02:05:46 (l3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Use "sieve of eratosthenes" and find prime numbers that is greater than M and smaller than N all the numbers we want is multiplication of these prime number.
Well but i think it's not possible to find the prime numbers till N!.(N factorial)
I think you can calculate instead the count of numbers that have prime factors smaller than M in the range 2 to N! and substract it from N! - 1. Now let the primes smaller than M pe p1, ..., pk, then by simple inclusion, exclusion the quantitiy you want is equal to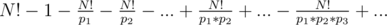 which is similar to euler's toitient function formula and you can write it as
which is similar to euler's toitient function formula and you can write it as 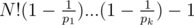 .
.
I hope this is correct.
can you post the link of this problem?
I think there's no way to solve this problem right now. Since U need to find all the prime numbered from M to N!. Let the count be X, our answer is 2^X -1.
Here is the problem link : https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=2435