I have a question , need fast to do to two types of operations:
update: 1 x y element on position x become y;
query : 2 x y number of distinct numbers from the interval [ x , y ];
How to solve this problem,can someone help me??
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 22:57:28 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
Where is this problem from?
It's a subproblem that I have to solve in problem that was given at regional olympiad.
Can you give the link to the problem?
You can solve this problem with segment trees where each node of your segment tree is a set.
Won't be fast enough. it will be O(N*logN) for merging nodes (the sets).
So then range query will be answered in O(logN*logN*N). Also the building of the tree will be O(N*N*log(N)).
take new array.for each element of first array find next index where same element stand,if it is,else use value INF. for query l,r you should answer question: how many elements is greater than r in range (l,r) in new array? it is standart segment tree or other data structure problem,and can be solved in O(n * logn) .for update operation you should change next and previus values of modified element.
What u mean by next index? Can you plz elaborate.
for array: 4,1,4,6,1,6,6
second array: 3,5,INF,6,INF,7,INF
for query (4,7) only 2 elements is greater than 7 so answer is 7(as 6,1)
"how many elements is greater than r in range (l,r) in new array? it is standart segment tree or other data structure problem,and can be solved in O(n * logn)"
How can we do that? Online and O(n * log(n))?
sorry I was wrong,I asked here same question,it can be solved in O(n * log(n)2) .I missed one log(n) :)
Online?
yes
There's a solution which is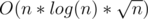
, and O(n * log(n)2) with treap + segment tree. What is the solution for online and just segment tree? Are you sure about it?
I mean: " it is standart segment tree or other data structure problem" only segment tree can't solve this,but as you say(with your complexity and with this data structures) you can update,and it will be online
Can you describe the way using segment tree + bst?
I can't figure it.
Without update, solution is segment tree + vector. You need to delete and add to vector, and it have to be sorted. You can use treap for it.
MO's algorithm. Since you're not updating the array, offline solution is possible. However, this has n*(sqrt(n)) complexity.
Are you sure?
1 x y element on position x become y;sorry no being:
element on position x become y.
When I wrote this comment, it was "being" and now its "become" so not my fault