Привет всем! У меня появился такой вопрос: можно ли найти значение 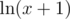 , зная чему равен
, зная чему равен 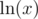 и не вычисляя значения x, ибо оно может быть воистину гигантским?
и не вычисляя значения x, ибо оно может быть воистину гигантским?
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
15:30:06
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
15:30:06
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 30.11.2024 02:04:55 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Насколько я знаю, если a, b > 0 и a > b, тогда ln(a + b) = ln(a) + ln(1 + b / a); В вашем случае, если x > 0, тогда ln(x + 1) = ln(x) + ln(1 + 1 / x). Причем если x воистину гигантское, то ln(1 + 1 / x) ~ 0, и им можно пренебречь. Хотя тут не уверен, если нужно абсолютно точное решение, то я его не знаю :)
Забавно, но ты просто получил что ln(x) ~ ln(x+1) :)
Нет, ну понятно, что погрешность нарастает, и выльется в большие числа уже скоро, но я не знаю как из ln(x) получить ln(x + 1) абсолютно точно :) + это работает, только если X и правда число очень большое :)
UPD: Это разные функции, но ничего. Уверен, они дают повод для размышлений.
for very large x.
Of course, if x is very-very big, then up to precision of your data types, the difference is negligible (if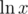 is in the order of 103,
is in the order of 103,  is in the order of 10 - 400) and you can just write
is in the order of 10 - 400) and you can just write 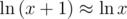 .
.
It can be shown that error is asymptotically small enough.
Thus if x if large enough you may say that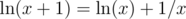 and get the error of order not more than O(1 / x2).
and get the error of order not more than O(1 / x2).
Actually you could take first k elements of Taylor series and precision will be